O padrão IEEE 754, adotado em 1985, define regras de normalização para operações e representações de números binários de ponto flutuante. Desde então, passou por modificações e continua sendo a referência para cálculos precisos e confiáveis na computação.
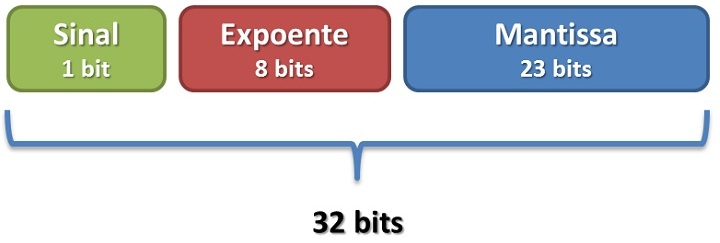
O padrão é composto por uma sequência de 32 bits, divididos da seguinte maneira:
✍️ Exemplo: Vamos utilizar como exemplo o número 999,99910 para demonstrar a conversão para o padrão IEEE 754.
Para converter um número decimal para binário no formato IEEE 754, são necessários os seguintes passos:
🔴 PASSO #1: Definição do sinal.
✍️ bit 1 – números negativos ou bit 0 – números positivos
Como 999,99910 é um número positivo, o bit de sinal será 0 (zero).
🔴 PASSO #2: Conversão do número decimal para binário.
🔴 PASSO #3: Escrever o número binário resultante em notação científica e separar a mantissa.
![]()
a vírgula foi deslocada nove “casas” para a esquerda.
Portanto, a mantissa é a parte “fracionária” do número binário normalizado:
🔴 PASSO #4: Calcular o expoente.
O expoente corresponde ao número de deslocamentos da vírgula para a esquerda mais 127, ou seja:
9 + 127 = 136 = 10001000
Logo, o expoente = 10001000
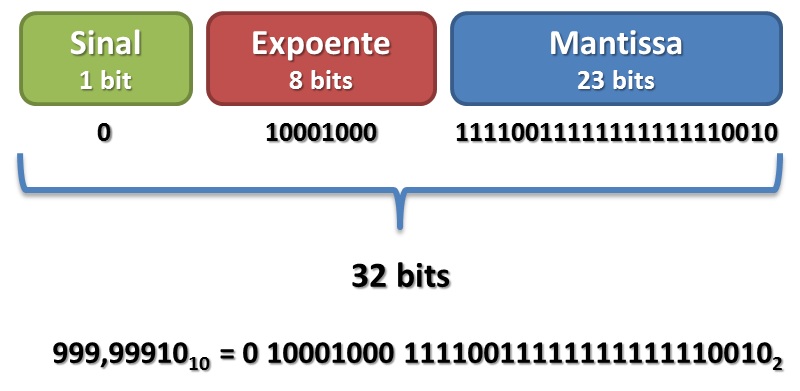
🔴 PASSO #5: Escrever o número binário no padrão IEEE 754.
Finalmente, temos que:
Dúvidas e sugestões serão bem-vindas!
*Atualizado em 15 de julho de 2023




Como eu identificou um NaN (not a number) ?
como é representado o zero e números infinitos neste formato?
Ah, tão simples e entendível com você explicando. Meu professor arrumou uns arranjos tão estranhos para explicar a “bias” (sobre o expoente) que eu estava achando que era um bicho de sete cabeças.
Akissel, de fato, o cálculo em si não é complicado, mas entender como a máquina faz a mágica toda não é algo tão trivial, e depende da abordagem do professor.
Valeu!
Tem como fazer a conversão oposta? Em vez de Decimal para IEEE 754, fazer o IEEE 754 para Decimal?
Amigão, vou tentar postar aqui essa conversão.