Vamos criar um algoritmo para resolver uma equação do 2º Grau?

✅ PROBLEMA: Desenvolva um algoritmo que calcule as soluções de uma equação do 2º grau qualquer.

• • Deve ser feito um teste para verificar se a equação fornecida pelo operador é ou não uma equação do 2º grau.
  • Verifique também se, a partir do valor de delta (∆) encontrado, a equação dada possui raízes reais ou não.

📚 O que é uma equação do 2º Grau?

Uma equação do segundo grau é uma equação algébrica da forma ax² + bx + c = 0, onde a e b são os coeficiente, c é o termo independente e x é a incógnita. Uma equação do segundo grau pode ser resolvida usando a fórmula geral:

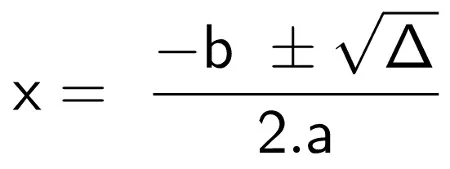
Onde:

• • a, b e c são, respectivamente, os coeficientes de x e o termo independente da equação ax² + bx + c = 0. Observe que, se a = 0, teremos: 0.x² + bx + c = bx + c = 0 (Equação do 1º Grau);
  • e ∆ é o discriminante, dado por: ∆ = b² – 4 . a . c.

Individualmente as raízes são dadas por:

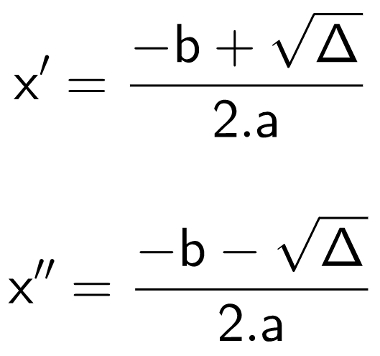
Contudo, a presença ou ausência de raízes reais depende do valor do discriminante (∆ = b² – 4 . a . c):

• • Se ∆ > 0, a equação tem duas raízes reais distintas, x’ e x”;
  • Se ∆ = 0, a equação tem uma raiz real única dada por: -b/2.a;
  • Se ∆ < 0 negativo, a equação não tem raízes reais.

RESUMINDO…

Para resolver uma equação do 2º grau da forma ax² + bx + c = 0:

1. 1. Utilizamos a fórmula geral: x = (-b ± √∆) / 2.a.
   2. Substituímos os valores de a, b e c na fórmula.
   3. Calculamos o valor de delta (∆ = b² – 4.a.c).
   4. Verificamos se delta é positivo, negativo ou zero.
      • Caso delta seja positivo, temos duas raízes reais e distintas, dadas por x‘ = (-b – √∆) / 2.a e x” = (-b + √∆) / 2.a, respectivamente.
      • Caso delta seja igual a zero, temos uma raiz real e dupla, dada por -b/2.a.
      • Caso delta seja negativo, não há raízes reais.

Exemplo: Resolvendo a equação x² + 5x + 6 = 0.

1. 1. Temos: a = 1, b = 5 e c = 6.
   2. Calculamos o discriminante:
      ∆ = b² – 4ac
      ∆ = 5² – 4 .1 .6
      ∆ = 25 – 24
      ∆ = 1
   3. Como ∆ > 0, temos duas raízes reais e distintas.
   4. Utilizando a fórmula geral:
      x = (-b ± √∆) / 2a
      x = (-5 ± √(1)) / 2
      x = (-5 ± 1) / 2
      Temos:
      x’ = (-5 + 1) / 2
      x’ = -2
      e
      x” = (-5 – 1) / 2
      x” = -4
   5. Concluímos que as raízes da equação x² + 5x + 6 = 0 são -2 e -4.

💻 Algoritmo: Portugol | VisuaAlg.

⚠️  Exercícios para testar o algoritmo. Clique aqui! ⚠️ 

—

Já sabemos que, para a equação ax² + bx + c = 0 ser considerada do 2º grau, o coeficiente a deve ser diferente de zero (a ≠ 0). O algoritmo com as alterações que verificam essa condição é mostrado abaixo. [As alterações feitas estão nas linhas 15, 33, 34 e 35, respectivamente.]

—
EXPLICANDO…

• Linha 1 – Aqui é dado um nome ao algoritmo com a palavra reservada algoritmo.
• Linhas 2, 3 e 4 – São informações adicionais (comentários) definidas com as duas barras, //, no começo de cada linha. Lembre-se: comentários são importantes para deixar seus algoritmos mais legíveis e são ignorados durante a execução do código.
• Linha 5 – A instrução var define que variáveis estão sendo declaradas.
• Linha 6 – são declaradas as seguintes variáveis: a, b, c, delta, x1, x2 do tipo real. Observe que nomes de variáveis não podem conter símbolos, caracteres especiais nem acentos, então, no lugar de ∆, x’ e x” declaramos delta, x1 e x2, respectivamente.
• Linhas 7 e 36 – As palavras reservadas inicio e fimalgoritmo, como seus nomes já dizem, indicam o início e o fim do algoritmo propriamente dito.
• Linhas 8 a 13 – Aqui ocorrem as entradas de dados por meio da exibição de uma mensagem, instruções escreva("a = "), escreva("b = ") e escreva("c = "); seguida da leitura do que foi digitado no teclado, instruções leia(a), leia(b) e leia(c).
• Linha 14 – Linha em branco; ignorada durante a execução do algoritmo.
• Linha 15 – A instrução se(a <> 0) entao verifica se a ≠ 0, e caso seja, serão executadas as linhas 16 a 32; se a = 0, será executada a linha 34, escreval("Não é uma equação do 2º grau!").
• Linha 16 – O valor de ∆ é calculado: delta <- b^2 - 4 * a * c.
• Linha 17 – Linha em branco; ignorada durante a execução do algoritmo.
• Linha 18 – Verifica se ∆ < 0. Se for verdadeiro, são executadas a linhas 19 e 20: escreval("DELTA = ", delta) e escreval("DELTA = ", delta), respectivamente.
• Linha 21 – Instrução senao: até aqui já sabemos que ∆ não é negativo (menor que zero) e nos resta saber se ele é igual a zero ou maior que zero…
• Linha 22 – Aqui fazemos o teste para saber se ∆ é igual a zero com a instrução se(delta = 0) entao, caso seja, existirá apenas uma raiz para a equação e será calculada na linha 23 com a instrução x1 <- -b/(2*a) e exibido na tela "DELTA = " seguido pelo valor de delta (linha 24), e "x' = x'' = " seguido pelo valor de x1 (linha 25).
• Linha 26 – Instrução senao: caso as condições nas instruções se anteriores não sejam atendidas, ou seja, ∆ não é menor que zero nem igual a zero, é calculado x1 através da fórmula x1 <- (-b - raizq(delta)) / (2 * a), linha 27, e x2 através da fórmula x2 <- (-b + raizq(delta)) / (2 * a), linha 28.
  • • O cálculo da raiz quadrada de ∆ é feito com a função raizq().
    • Em seguida, são exibidos na tela "x' = " seguido pelo valor de x1 e "x'' = " seguido pelo valor de x2, linhas 29 e 30.
      Observe que os valores das raízes calculadas serão exibidos com tamanho máximo de 6 caracteres (dígitos) dos quais 2 são reservados para casas decimais, conforme a formatação x1:6:2 e x2:6:2.
• Linha 31 – Instrução fimse: indica o fechamento do se é da linha 22. Cuidado: para cada se deve haver um fimse associado.
• Linha 32 – Instrução fimse: indica o fechamento do se é da linha 18.
• Linhas 33 e 34 – Instrução senao: verifique a explicação dada na linha 15.
• Linha 35 – Instrução fimse: indica o fechamento do se é da linha 15.
• Linha 36 – Instrução fimalgoritmo: marca o final do algoritmo.

—

🐍 Versão em Python

🔥 E para atiçar ainda mais sua curiosidade, podemos modificar o código acima em Python para que seja desenhado (plotado) o gráfico da equação do segundo grau dada! Vejamos:

Saída:

📈 Gráfico gerado:

—

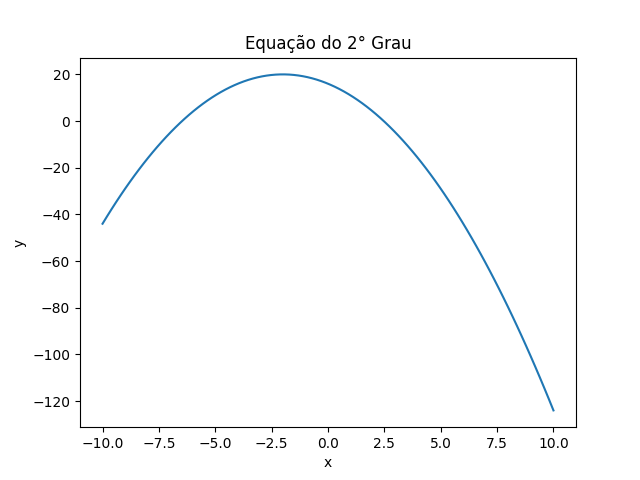
📚 Livros

• • Aprendendo Algoritmo com Visualg
    Rafael Soares de Almeida
    <https://amzn.to/3DeiwxN>
    

• • Introdução à linguagem Python
    José Augusto N. G. Manzano
    <https://amzn.to/3tS3A2Y>
    

• • Algoritmos: Lógica para Desenvolvimento de Programação de Computadores
    José Augusto N. G. Manzano e Jayr Figueiredo de Oliveira
    <https://amzn.to/43sGKic>

—

^{*Atualizado em 19 de julho de 2023}